Nelinearne enačbe in geometrija

Ogledali si bomo nekaj primerov uporabe metod za reševanje nelinearnih enačb v geometriji krivulj in ploskev v 2D in 3D.

Samopresečišče krivulje

Poišči samopresečišča različnih lissajousjevih krivulj. Lissajousjeva krivulja je podana parametrično z enačbama

\[(x(t), y(t)) = (a\sin(n t), b\cos(m t)).\]

Primer lissajoujeve krivulje za $n=3, m=2$

using Plots
x(t) = cos(3*t); y(t) = sin(2*t);
t = range(0, stop=2pi, length=100)
plot(x.(t), y.(t), grid=false, legend=:none)
t = range(0, stop=6, length=21)
# scatter!(x.(t), y.(t))
# annotate!([(x(tt)+0.05, y(tt)+0.05, "t=$tt") for tt in t])

Samopresečišče lahko poiščemo z Newtonovo metodo

dx(t) = -3sin(3t); dy(t) = 2cos(t);
f(t, s) = [x(t) - x(s), y(t) - y(s)]
Jf(t, s) = [dx(t) -dx(s); dy(t) -dy(s)]

let t0 = 1; s0 = 3
plot!([x(t0), x(s0)]; [y(t0), y(s0)], marker=:circle)
for i=1:5
  [t0, s0] = [t0, s0] - Jf(t0, s0)\f(t0, s0)
  plot!([x(t0), x(s0)], [y(t0), y(s0)], marker=:circle)
end
end # let
plot!(legend=false)

Območje konvergence

Konvergenca newtonove metode je odvina od začetnega približka.

Razdalja med dvema krivuljama

Naj bosta $K_1$ in $K_2$ parametrično podani krivulji

\[\begin{aligned} K_1 &: (x(t),y(t)),\quad t\in\mathbb{R}\cr K_2& : (\tilde{x}(s),\tilde{y}(s)),\quad s\in\mathbb{R}. \end{aligned}\]

Razdaljo med krivuljama lahko definiramo na različne načine

najmanjša razdalja $d(K_1, K_2) = \min_{x\in K_1, y\in K_2} d(x,y)$
hausdorffova razdalja

\[ d_h(K1, K2) = \max\left\{\max_{x\in K_2}\min_{y\in K_1}d(x,y), \max_{x\in K_1}\min_{y\in K_2}d(x,y) \right\}\]

Hausdorffova razdalja

Hausdorffova razdalja pove, koliko je lahko točka na eni krivulji največ oddaljena od druge krivulje. Če sta množici blizu v hausdorffovi razdalji, je vsaka točka ene množice blizu drugi množici. Medtem, ko je minimalna razdalja med dvema krivuljama vedno končna, pa je lahko hausdorffova razdalja tudi neskončna (na primer, če je ena krivulja omejena, druga pa neomejena).

Najlažje je poiskati minimalno razdaljo. Iščemo točki na krivuljah $(x(t_0),y(t_0))\in K_1$ in $(\tilde{y}(s_0),\tilde{y}(s_0))\in K_2$, za katere bo razdalja

\[d(t,s)=\sqrt{(x(t)-\tilde{x}(s))^2+(y(t)-\tilde{y}(s))^2}\]

najmanjša. Ker je koren naraščajoča funkcija, ga lahko pri iskanju minimuma brez škode izpustimo in obravnavamo funkcijo

\[D(t,s)=d(t,s)^2=(x(t)-\tilde{x}(s))^2+(y(t)-\tilde{y}(s))^2,\]

ki je bolj enostavna za računanje. Opazimo, da je razdalja odvisna le od parametrov $t$ in $s$. Dovolj je, da poiščemo vrednosti $(t_0, s_0)$, v katerih bo vrednost funkcije $d(t, s)$ oziroma $D(t, s)$ minimalna. Če je območje parametrov $(t, s)\in\mathbb{R}^2$ cela ravnina, bo najmanjša vrednost nastopila v lokalnem ekstremu, v katerem je tudi stacionarna točka funkcije $D(t, s)$. Iskanja lokalnega ekstrema se bomo lotili na dva različna načina, a še prej si oglejmo primer.

Primer

Poglejmo si primer dveh elips v ravnini

\[\begin{aligned} x(t) &= 2\cos(t)+\frac{1}{3}\cr y(t) &= \sin(t)+\frac{1}{4}\end{aligned}\]

\[\begin{aligned} \tilde{x}(s) &= \frac{1}{3}\cos(s)-\frac{1}{2}\sin(s)\cr \tilde{y}(s) &= \frac{1}{3}\cos(s)+\frac{1}{2}\sin(s)\end{aligned}\]

Narišimo ju z

using Plots
tocka(a) = tuple(a...)
K1(t) = [2*cos(t) + 1/3, sin(t) + 0.25]
K2(s) = [cos(s)/3 - sin(s)/2, cos(s)/3 + sin(s)/2]
t = LinRange(0, 2*pi, 60);
plot(tocka.(K1.(t)), label="K1")
plot!(tocka.(K2.(t)), label="K2")

Narišimo tudi graf funkcije $D(t,s)$ na pravokotniku $[0,2\pi]\times[0,2\pi].$

D(t, s) = sum((K1(t) - K2(s)).^2)
contourf(t, t, D, title="Kvadrat razdalje, v odvisnosti od parametrov")

Metoda najhitrejšega spusta

Metoda je sila enostavna. Najlažje si jo predstavljamo za iskanje lokalnega mimimuma nadmorske višine. Sestopili bi radi na dno kraške vrtače. Če se držimo metode najhitrejšega spusta, na vsakem koraku izberemo smer, v kateri je pobočje najbolj strmo. V jeziku funkcij to pomeni, da na vsakem koraku izberemo smer, v kateri funkcija najhitreje pada. To je ravno v nasprotni smeri gradienta funkcije. Lokalnemu minimumu funkcije $f(\mathbf{x})$ se lahko tako približamo z naslednjim zaporedjem približkov

\[\mathbf{x}_n=\mathbf{x}_{n-1}-h_n\bigtriangledown f(\mathbf{x}),\]

kjer je $\mathbf{x}=[x_1,\ldots,x_k]^T$ vektor spremenljivk, $h_n\in \mathbb{R}_+$ pa omejeno zaporedje, ki je lahko tudi konstantno.

using NumMat
dK1(t) = [-2sin(t), cos(t)]
dK2(s) = [-sin(s)/3 - cos(s)/2, -sin(s)/3 + cos(s)/2]
gradD = gradient_razdalje(K1, K2, dK1, dK2)
slika = contour(t, t, D, title="Zaporedje korakov gradientne metode")

let
x0 = [0.4, 3.3]
h = 0.2
priblizki = [tuple(x0...)]
for i=1:40
  x0 = x0 - h*gradD(x0)
  push!(priblizki, tuple(x0...))
end
scatter!(slika, priblizki)
end # let
slika #hide

Konvergenca je odvisna od zažetnega približka

Limita zaporedja $\mathbf{x}_n$ je zelo odvisna od začetnega približka $x_0$, pa tudi od izbire parametra $h_k$. Kaj lahko se nam zgodi, da bomo pristali v "napačnem" minimumu. Prav tako je konvergenca vedno počasnejša, bližje kot smo minimu.

Newtonova metoda

Fermat je med drugim dokazal izrek, ki pove, da je v lokalnem ekstremu vrednost odvoda vedno enaka 0. Isti izrek velja tudi za funkcije več spremenljivk, le da je v tem primeru gradient funkcije enak 0.

Ta izrek morda ni tako razvpit kot njegov zadnji izrek, je pa zato toliko bolj uporaben. Potreben pogoj za nastop lokalnega ekstrema je namreč vektorska enačba

\[\bigtriangledown D(s,t)=0,\]

ki je v našem primeru sistem dveh enačb z dvema neznankama

\[\begin{aligned} \frac{\partial D(t,s)}{\partial t} = 2(x(t)-\tilde{x}(s))\dot{x}(t) + 2(y(t)-\tilde{y}(s))\dot{y}(t) &= 0\cr \frac{\partial D(t,s)}{\partial s} = -2(x(t)-\tilde{x}(s))\dot{\tilde{x}}(s) - 2(y(t)-\tilde{y}(s))\dot{\tilde{y}}(s) &= 0.\end{aligned}\]

Rešitev zgornjega sistema lahko poiščemo numerično z uporabo Newtonove metode za sisteme enačb. Podobno kot pri Newtonovi metodi za eno spremenljivko potrebujemo odvod, vendar imamo pri več enačbah z več spremenljivkami opravka z odvodom vektorske funkcije več spremenljivk. Sistem lahko zapišemo kot eno samo vektorsko enačbo

\[\mathbf{F}(t,s)=0,\]

kjer pa je

\[\mathbf{F}(t,s)=\begin{pmatrix} F_1(t,s)\cr F_2(t,s) \end{pmatrix} = \begin{pmatrix} \frac{\partial D(t,s)}{\partial t}\cr \frac{\partial D(t,s)}{\partial s} \end{pmatrix}\]

vektorska funkcija. Odvod funkcije $\mathbf{F}$ lahko predstavimo z linearno preslikavo, ki je dana z matriko (imenovano tudi Jacobijeva matrika sistema):

\[J(\mathbf{F}(t,s))=\begin{pmatrix} \frac{\partial F_1(t,s)}{\partial t} & \frac{\partial F_1(t,s)}{\partial s}\cr \frac{\partial F_2(t,s)}{\partial t} & \frac{\partial F_2(t,s)}{\partial s} \end{pmatrix}\]

Pri Newtonovi metodi sestavimo zaporedje približkov definirano z naslednjo rekurzivno formulo

\[\mathbf{x}_n = \mathbf{x}_{n-1} - J(\mathbf{F}(\mathbf{x}_{n-1}))^{-1}\cdot\mathbf{F}(\mathbf{x}_{n-1}), \quad \mathbf{x}_n = (t_n,s_n)^T.\]

Če je zaporedje $\mathbf{x}_n$ konvergentno, potem je limita rešitev enačbe $\mathbf{F}(\mathbf{x})=0$. Zaporedje $\mathbf{x}_n$ ponavadi zelo hitro konvergira, zato za rešitev potrebujemo relativno malo korakov. Prav tako Newtonovo iteracijo hitro sprogramiramo, saj je dovolj že ena zanka.

Vrnimo se k našem primeru razdalje med dvema krivuljama. Jacobijeva matrika je v tem primeru kar matrika drugih odvodov funkcije razdalje $D(t,s)$

\[J(\mathbf{F}(t,s)) = \begin{pmatrix} \frac{\partial^2 D(t,s)}{\partial t^2} & \frac{\partial^2 D(t,s)}{\partial s\partial t}\cr \frac{\partial^2 D(t,s)}{\partial t\partial s} & \frac{\partial^2 D(t,s)}{\partial s^2} \end{pmatrix}.\]

Enačbe za druge odvode $D(s,t)$ hitro izpeljemo iz gradienta $D(t,s)$

\[\begin{aligned} \frac{\partial^2 D(t,s)}{\partial t^2}&=2(\ddot{x}(t)(x(t)-\tilde{x}(s)) +\dot{x}^2(t) + \ddot{y}(t)(y(t)-\tilde{y}(s)) +\dot{y}^2(t))\cr \frac{\partial^2 D(t,s)}{\partial s^2} &= 2(-\ddot{\tilde{x}}(s)(x(t)-\tilde{x}(s)) +\dot{\tilde{x}}^2(s) - \ddot{\tilde{y}}(s)(y(t)-\tilde{y}(s)) +\dot{\tilde{y}}^2(s))\cr \frac{\partial^2 D(t,s)}{\partial t\partial s} &=-2(\dot{\tilde{x}}(s)\dot{x}(t)+ \dot{\tilde{y}}(s)\dot{y}(t). \end{aligned}\]

Poleg tega velja

\[\frac{\partial^2 D(t,s)}{\partial s\partial t}= \frac{\partial^2 D(t,s)}{\partial t\partial s}.\]

Preskusimo sedaj Newtonovo metodo za naš primer dveh elips. Funkcija, katere ničle iščemo je kar enaka gradientu. Napisati moramo še funkcijo, ki vrne Jacobijevo matriko.

Avtomatsko odvajanje

Iskanje odvodov postane hitro zamudno in mimogrede se pri računanju človek zmoti. Na srečo si lahko pri tem si lahko pomagamo z avtomatskim odvajanjem, ki programsko iz programa za funkcijo generira program za odvod. Julija ima več knjižnic za ta namen, mi bomo uporabili ForwardDiff.jl.

using ForwardDiff
D2((t,s)) = sum((K1(t)-K2(s)).^2)
gradD2(x) = ForwardDiff.gradient(D2, x)
hessD2(x) = ForwardDiff.hessian(D2, x)

slika = contour(t, t, (t, s)-> D2((t,s)), title="Zaporedje korakov Newtonove metode")

x0 = [1., 4.]
priblizki = [tuple(x0...)]

let
x = x0
for i=1:10
  x = x - hessD2(x)\gradD2(x)
  push!(priblizki, tuple(x...))
end
end # let
scatter!(slika, priblizki)

plot(tocka.(K1.(t)), label="K1", aspect_ratio=:equal, title="Sedlo")
plot!(tocka.(K2.(t)), label="K2")
t0, s0 = priblizki[end]
plot!(tocka.([K1(t0), K2(s0)]), marker=:circle, label="zadnji korak")

Konvergenčno območje

Konvergenca tako gradientne kot tudi newtonove metode je zelo odvisna od začetnega približka.

julia> using Plots;
julia> x, y, Z = konvergencno_obmocje((0, 2pi, 0, 2p), 
  x -> newton(gradD2, hessD2, x; maxit=20, tol=1e-3), n=300, m=300);
julia> heatmap(x, y, Z')
julia> contour!(x, y, (x,y)->razdalja((x,y)))
julia> maximum(Z)
6157.0

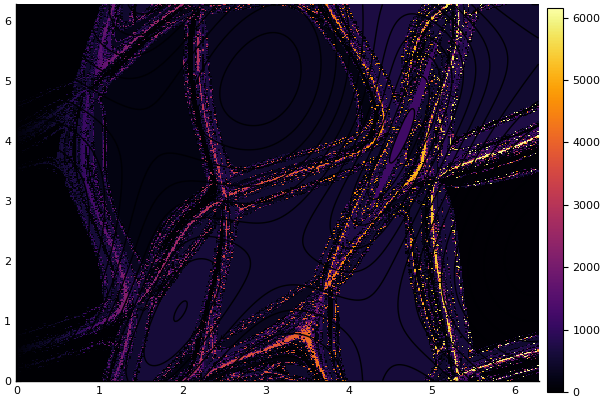
Konvergenca newtonove metode

Konvergenčno območje newtonove metode je razdeljeno. Iz slike je razvidno, da je veliko različnih približkov (6157), h kateri konvergira newtonova metoda na območju $[0,2\pi]\times[0, 2\pi]$, čeprav je na tem območju le nekaj rešitev.

julia> using Plots;
julia> x, y, Z = konvergencno_obmocje((0, 2pi, 0, 2pi),
       x -> spust(grad, x; maxit=1000, tol=1e-3), tol=1e-1, n=200, m=200)
julia> heatmap(x, y, Z')
julia> contour!(x, y, (x,y)->razdalja((x,y)))
julia> maximum(Z)
8.0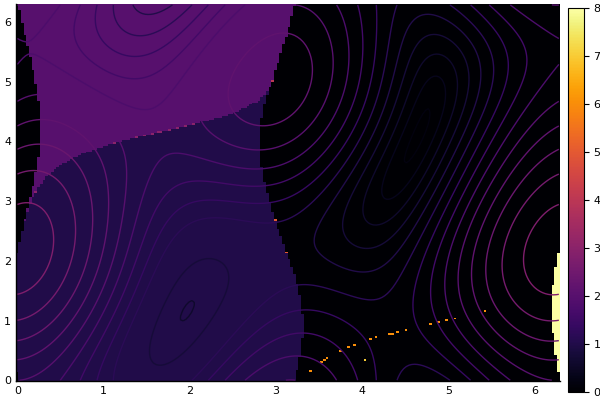

Konvergenca gradientne metode

Za razliko od newtonove metode, je konvergenčno območje gradientne metode precej bolj predvidljivo.

Drugi primeri nelinearnih enačb iz 3D geometrije

presečišče dveh krivulj v 2D
presečišče krivulje in ploskve v 3D
presečišče dveh ploskev v 3D